Análisis Multinivel Bayesiano

Estudio sobre análisis multinivel bayesiano de rendimiento en matemáticas entre 10 centros educativos.

Una Aproximación Bayesiana al Análisis Multinivel

El análisis multinivel es un procedimiento estadístico que permite dar cuenta de la idiosincrasia y, por ende, de la variabilidad no solo de los individuos, sino de sus agrupaciones: instituciones, centros educativos, territorios, etc. Todo depende de la articulación teórica desde la cual se parta.

Por ejemplo, se puede establecer como objeto de estudio a un grupo de personas formado por varios individuos y analizar las diferencias entre ellos (nivel 1), al mismo tiempo que se examinan las diferencias entre los grupos en los que dichos individuos se encuentran (nivel 2). Asimismo, es posible ampliar el modelo incorporando niveles adicionales, como territorios o países (nivel 3), para captar la variabilidad asociada a estructuras más complejas.

Esto da cuenta de la flexibilidad y utilidad de los análisis multinivel, característica muy apreciada por el enfoque bayesiano dado que:

“La propia lógica de los métodos bayesianos se adapta de forma natural a los métodos de efectos aleatorios, en los que los parámetros pasan a ser considerados variables aleatorias.”
(Revuelta & Ximénez, 2014)

Por ello, este trabajo se compromete a explorar las posibilidades que ofrece el análisis multinivel bayesiano con datos recogidos en 10 centros educativos sobre el rendimiento de los estudiantes en matemáticas, centrando nuestro interés en la variabilidad existente entre centros, pero también en cada centro.

Método

Los datos se recogieron en 10 centros distintos (schid) cuya muestra total es de 260 estudiantes. Las variables medidas son:

Rendimiento en matemáticas: puntuación en una escala de 0-100. Variable dependiente (math).
Horas de deberes de matemáticas: número de horas diarias que dedica cada estudiante. Variable predictora de primer nivel (homework).

Puesto que nuestro interés reside en la exploración de la flexibilidad de los modelos multinivel, se han estimado 3 modelos:

Modelo 0: Intersecciones aleatorias sin variable predictora

No se tiene en cuenta ninguna variable predictora. Las intersecciones se consideran aleatorias entre centros.
Parámetros estimados:

Parte fija de la intersección: \(\mu_{0}\)
Parte aleatoria de la intersección: \(\omega^2_{0}\)
Varianza del error: \(\sigma^2_{e}\)

Este modelo propone que las medias en el desempeño en matemáticas difieren entre centros, sin considerar ninguna variable predictora. Es el modelo nulo.

Modelo 1: Intersecciones aletorias, pendientes fijas con una variable predictora de primer nivel

Se introduce una variable predictora de primer nivel (homework). Se consideran intersecciones aleatorias y pendientes fijas.
Parámetros estimados:

Parte fija de la intersección: \(\mu_{0}\)
Parte aleatoria de la intersección: \(\omega^2_{0}\)
Parte fija de la pendiente: \(\mu_{1}\)
Varianza del error: \(\sigma^2_{e}\)

Este modelo propone que las medias en el desempeño en matemáticas difieren entre centros teniendo en cuenta homework, pero asume que su efecto es el mismo en todos los colegios.

Cadenas de Markov Monte Carlo de los parámetros del Modelo 1. — Figura 4. Cadenas de Markov Monte Carlo (MCMC) de los parámetros del Modelo 1.

Figura 5. Gráfica de pares MCMC que muestra las distribuciones marginales (diagonal) y las correlaciones entre parámetros (scatterplots fuera de la diagonal) del Modelo 1.

Figura 6. Posterior Predictive Checks del Modelo 1.

Modelo 2: Intersecciones y pendientes aletorias con una variable predictora de primer nivel

Igual al Modelo 1, pero con pendientes aleatorias entre centros.
Parámetros estimados:

Parte fija de la intersección: \(\mu_{0}\)
Parte aleatoria de la intersección: \(\omega^2_{0}\)
Parte fija de la pendiente: \(\mu_{1}\)
Parte aleatoria de la pendiente: \(\omega^2_{1}\)
Covarianza intersección–pendiente: \(\omega_{01}\)
Varianza del error: \(\sigma^2_{e}\)

Este modelo propone que las medias en el desempeño en matemáticas difieren entre centros teniendo en cuenta homework, pero ahora se asume que el efecto de esta variable no es el mismo en todos los colegios.

ANEXO: Script de R en combinación con lenguaje Stan (cmdstanr)

# ==============================================================================
# HEADER: Script Information
# ==============================================================================
# Script Name: cmdstanr_version.R
# Author: Alicia Gil Matute
# Position: Data Scientist
# Date Created: 2025-03-07
# Email: aliciagilmatute@gmail.com
# ==============================================================================

# ==============================================================================
# SECTION 1: Load packages
# Libraries necessary for the script to function
# ==============================================================================

library(MASS)          # Multivariate gaussian distribution
library(cmdstanr)      # Estimate bayesian models in Stan (better than rstan)
library(posterior)     # Extract summaries
library(loo)           # WAIC and LOO estimates
library(haven)
library(bayesplot)
library(cowplot)
library(ggplot2)
library(blavaan)

# ==============================================================================
# SECTION 2: Load Data
# ==============================================================================

mlmdata <- read_dta("https://stats.idre.ucla.edu/stat/examples/imm/imm10.dta")

x <- 1:10

mlmdata$schid <- as.factor(mlmdata$schid)
levels(mlmdata$schid) <- as.character(x)
str(mlmdata)

View(mlmdata)


data_stan <- list(N = nrow(mlmdata), 
                  J = length(unique(mlmdata$schid)),
                  schid = as.numeric(mlmdata$schid), 
                  homework = mlmdata$homework, 
                  math = mlmdata$math)

is.na(data_stan)

hist(data_stan$schid)
hist(data_stan$homework)
hist(data_stan$math)


# ==============================================================================
# SECTION 3: Estimate bayesian multilevel model 
# Model 0: No predictor variable and Random Intercepts
# ==============================================================================

#Priors poco informativas:

#beta0~normal(0,10);
#sigma_e~gamma(1,0.5);    
#sigma_u0~gamma(1,0.5);
#u0~normal(0,sigma_u0);

# Compilamos el modelo

bmultinivel_0 <- cmdstan_model(stan_file = "model0_cmdstanr_version.stan")

bmultinivel_0f <- bmultinivel_0$sample(
  
  data = data_stan,       # Stan data
  chains = 4,            # Number of chains
  parallel_chains = 4,   # Number of parallel chains
  iter_warmup = 500,     # Adaptation iterations
  iter_sampling = 1500,  # Sampled iterations
  refresh = 500,         # Progress bar at 500 iterations
  init = 0)              # All starting values = 0

#necesitamos extraer el posterior para visualizar las cadenas de Markov

posterior_samples0 <- bmultinivel_0f$draws()

mcmc_trace(posterior_samples0, pars = c("beta0","sigma_u0","sigma_e"))

# Posterior distribution: pairs plots
mcmc_pairs(posterior_samples0, pars=c("beta0","sigma_u0","sigma_e"), diag_fun = "hist", 
           off_diag_fun = "scatter", off_diag_args = list(alpha = 0.5))

mcmc_intervals(posterior_samples0, pars =c("beta0","sigma_u0","sigma_e") )

#escuelas

params <- paste0("u0[", 1:10, "]")

mcmc_trace(posterior_samples0, pars = params)

mcmc_hist(posterior_samples0, pars=params)

#mcmc_scatter(posterior_samples, pars=c("u0[1]","u0[2]"))

mcmc_intervals(posterior_samples0, pars = params)


#Resultados 

bmultinivel_0f$summary()

#EL AJUSTE A LOS DATOS (equivalente al ajuste global) con la cmdstanr SE EVALUA CON PPMC:
#¿Podemos distinguir los datos observados de datos simulados desde el modelo (math_rep)?


# ==============================================================================
# SECTION 3.b: Posterior Predictive Model Check (PPMC) MODELO 0
# ==============================================================================

# Extraer y_rep correctamente desde CmdStanR
y_rep_0 <- as_draws_matrix(bmultinivel_0f$draws("y_rep"))

# Seleccionar solo 100 iteraciones aleatorias (iteraciones)
set.seed(123)  # Para reproducibilidad
y_rep_subset_0 <- y_rep_0[sample(1:nrow(y_rep_0), 100), ]

# Verificar dimensiones
dim(y_rep_subset_0)  # Debería ser (100, 300)

# Número de colegios
J <- length(unique(data_stan$schid))

# Lista para almacenar los gráficos
posterior_plots_list_0 <- vector(mode = "list", length = J)

# Generar gráficos PPMC para cada colegio
for(j in 1:J){
  posterior_plots_list_0[[j]] <- ppc_dens_overlay(
    y = data_stan$math[data_stan$schid == j],        # Datos reales del colegio j
    yrep = y_rep_subset_0[, data_stan$schid == j]  # Simulaciones para colegio j
  ) + 
    labs(title = paste("Colegio", j))
}

# Mostrar los gráficos juntos
cowplot::plot_grid(plotlist = posterior_plots_list_0)


#####IMPORTANTE##########

#No tiene sentido obtenerlo para beta0, sigma_uo y sigma_e porque son parametros de la distribucion (es un valor puntual "inferido"). En todo caso podria tener sentido obtenerlo para la beta0 ya que es la media de matematicas en las escuelas, pero es mas informativo tenerlo para cada escuela


# ==============================================================================
# SECTION 4: Estimate bayesian multilevel model 
# Model 1: Predictor variable and Random Intercepts and fixed Slopes
# ==============================================================================

#Priors poco informativas:

#beta[1]~normal(0,10);
#beta[2]~normal(0,10);
#sigma_e~gamma(1,0.5); 
#sigma_u0~gamma(1,0.5);
#u0~normal(0,sigma_u0);


# Compilamos el modelo

bmultinivel_1  <- cmdstan_model(stan_file = "model1_cdmstanr_version.stan")

bmultinivel_1f <- bmultinivel_1$sample(
  
  data = data_stan,       # Stan data
  chains = 4,            # Number of chains
  parallel_chains = 4,   # Number of parallel chains
  iter_warmup = 500,     # Adaptation iterations
  iter_sampling = 1500,  # Sampled iterations
  refresh = 500,         # Progress bar at 500 iterations
  init = 0)              # All starting values = 0


#necesitamos extraer el posterior para visualizar las cadenas de Markov

posterior_samples1 <- bmultinivel_1f$draws()

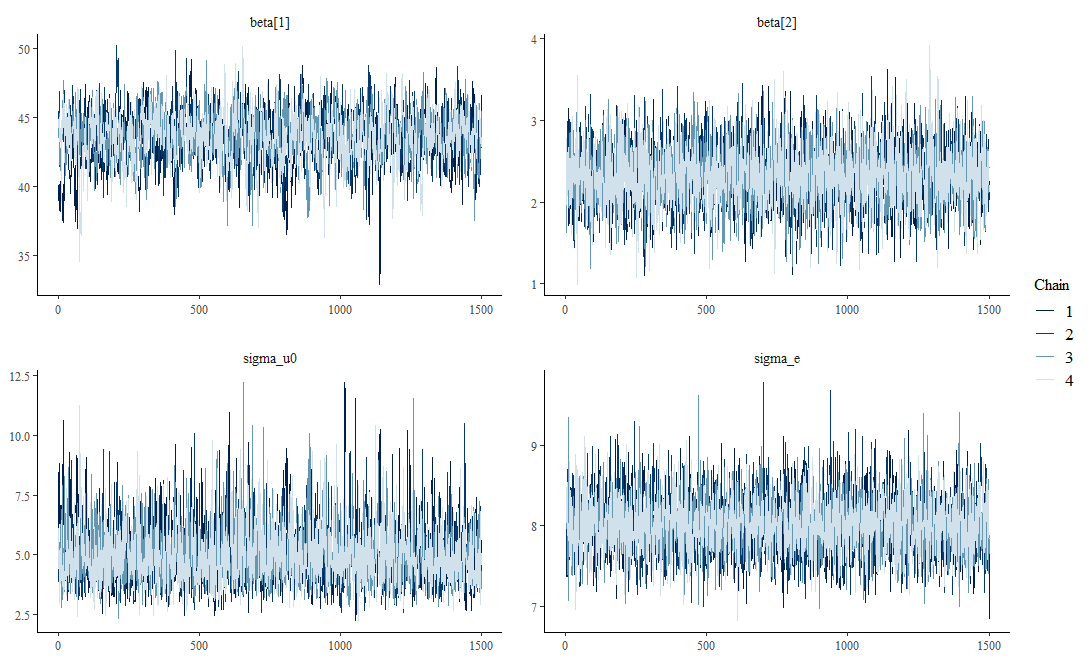
mcmc_trace(posterior_samples1, pars = c("beta[1]","beta[2]","sigma_u0","sigma_e"))

# Posterior distribution: pairs plots

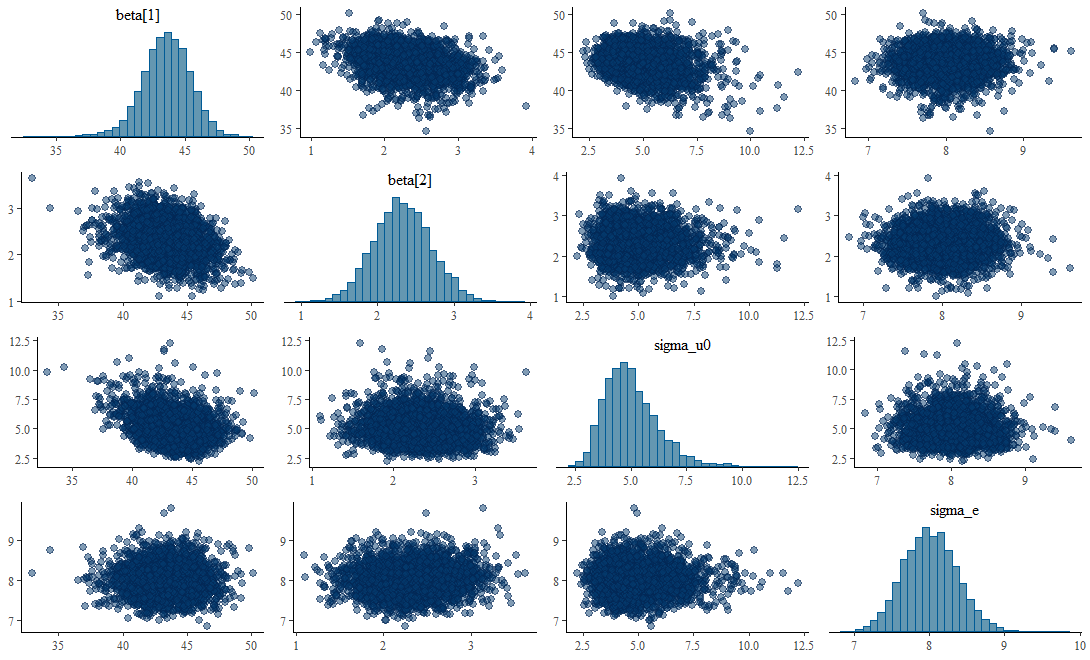
mcmc_pairs(posterior_samples1, pars=c("beta[1]","beta[2]","sigma_u0","sigma_e"), 
diag_fun = "hist",  off_diag_fun = "scatter", off_diag_args = list(alpha = 0.5))

mcmc_intervals(posterior_samples1, pars =c("beta[1]","beta[2]","sigma_u0","sigma_e") )

#escuelas

params <- paste0("u0[", 1:10, "]")

mcmc_trace(posterior_samples1, pars = params)

mcmc_hist(posterior_samples1, pars=params)

#mcmc_scatter(posterior_samples, pars=c("u0[1]","u0[2]"))

mcmc_intervals(posterior_samples1, pars = params)

#Resultados 

bmultinivel_1f$summary()

# ==============================================================================
# SECTION 4.b: Posterior Predictive Model Check (PPMC) MODELO 1 
# ==============================================================================

# Extraer y_rep correctamente desde CmdStanR
y_rep_1 <- as_draws_matrix(bmultinivel_1f$draws("y_rep"))

# Seleccionar solo 100 iteraciones aleatorias (iteraciones)
set.seed(123)  # Para reproducibilidad
y_rep_subset_1 <- y_rep_1[sample(1:nrow(y_rep_1), 100), ]

# Verificar dimensiones
dim(y_rep_subset_1)  # Debería ser (100, 300)

# Número de colegios
J <- length(unique(data_stan$schid))

# Lista para almacenar los gráficos
posterior_plots_list_1 <- vector(mode = "list", length = J)

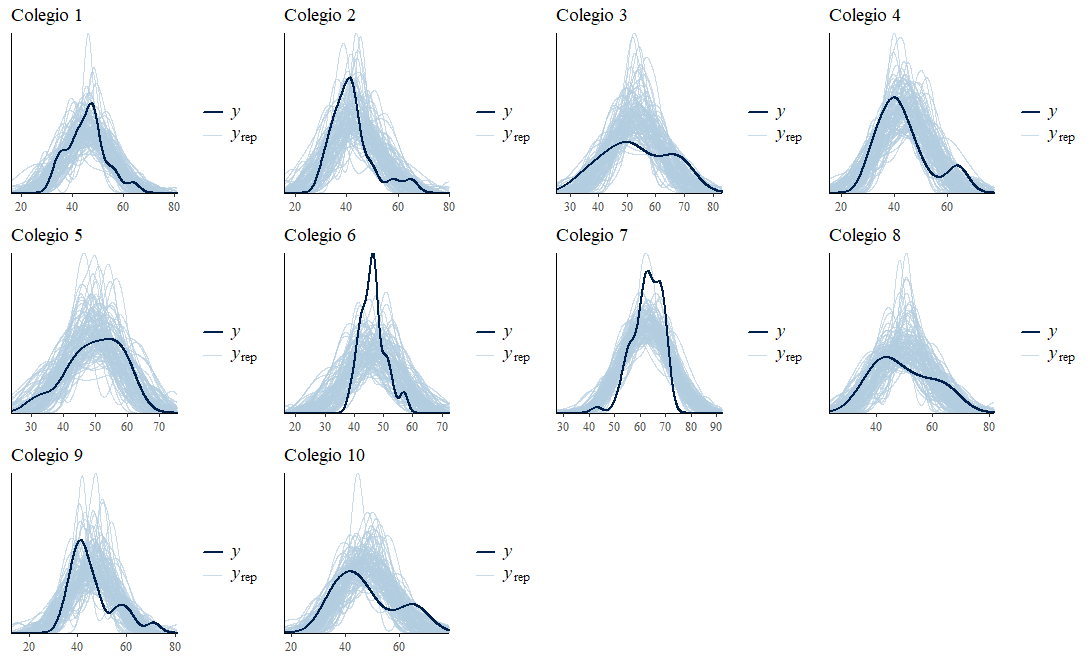
# Generar gráficos PPMC para cada colegio
for(j in 1:J){
  posterior_plots_list_1[[j]] <- ppc_dens_overlay(
    y = data_stan$math[data_stan$schid == j],        # Datos reales del colegio j
    yrep = y_rep_subset_1[, data_stan$schid == j]  # Simulaciones para colegio j
  ) + 
    labs(title = paste("Colegio", j))
}

# Mostrar los gráficos juntos
cowplot::plot_grid(plotlist = posterior_plots_list_1)


# ==============================================================================
# SECTION 4.c: Comparacion de modelos (capacidad predictiva)
# ==============================================================================

loo_1f  <- loo(x = bmultinivel_0f$draws("log_lik"))
loo_2f  <- loo(x = bmultinivel_1f$draws("log_lik"))
loo_compare(loo_1f, loo_2f)


# ==============================================================================
# SECTION 5.a: Estimate bayesian multilevel model 
# Model 2: Predictor variable and Random Intercepts and fixed Slopes
# ==============================================================================

#Priors poco informativas:

#  L_u ~ lkj_corr_cholesky(1);   
#to_vector(z_u) ~ normal(0, 1);
#beta~normal(0,10);
#sigma_e~gamma(1,0.5); 
#sigma_u~gamma(1,0.5);


bmultinivel_2  <- cmdstan_model(stan_file = "model2_cmdstanr_version.stan")

bmultinivel_2f <- bmultinivel_2$sample(
  
  data = data_stan,       # Stan data
  chains = 4,            # Number of chains
  parallel_chains = 4,   # Number of parallel chains
  iter_warmup = 500,     # Adaptation iterations
  iter_sampling = 1500,  # Sampled iterations
  refresh = 500,         # Progress bar at 500 iterations
  init = 0)              # All starting values = 0


#necesitamos extraer el posterior para visualizar las cadenas de Markov

posterior_samples2 <- bmultinivel_2f$draws()

#L_U[1,1] y L_u[1,2] no ha convergido pero L_u[2,1] si

mcmc_trace(posterior_samples2, pars = c("beta[1]","beta[2]","sigma_u[1]","sigma_u[2]","sigma_e",
                                        "L_u[1,1]","L_u[2,1]","L_u[2,2]"))

# Posterior distribution: pairs plots

mcmc_pairs(posterior_samples2, pars=c("beta[1]","beta[2]","sigma_u[1]","sigma_u[2]","sigma_e"), 
           diag_fun = "hist",  off_diag_fun = "scatter", off_diag_args = list(alpha = 0.5))

mcmc_pairs(posterior_samples2, pars=c("L_u[1,1]","L_u[2,1]","L_u[2,2]"), 
           diag_fun = "hist",  off_diag_fun = "scatter", off_diag_args = list(alpha = 0.5))

mcmc_intervals(posterior_samples2, pars =c("beta[1]","beta[2]","sigma_u[1]","sigma_u[2]","sigma_e"))

mcmc_intervals(posterior_samples2, pars =c("L_u[1,1]","L_u[2,1]","L_u[2,2]"))


#escuelas

params <- paste0("u0[", 1:10, "]")


mcmc_trace(posterior_samples2, pars = params)

mcmc_hist(posterior_samples2, pars=params)

#mcmc_scatter(posterior_samples, pars=c("u0[1]","u0[2]"))

mcmc_intervals(posterior_samples2, pars = params)

#Resultados 

bmultinivel_2f$summary()
bmultinivel_2f$summary("R")
bmultinivel_2f$summary("u0")


#en el script de stan se puede indicar directamente que calcule la media de cada colegio a partir
#de cada u0[j]

#Los parametros de nuestr interés son:
#beta[1]: parte fija interseccion
#beta[2]: parte fija pendientes
#sigma_u[1]: parte aleatoria interseccion
#sigma_u[2]: parte aleatoria pendientes
#R[1,2]: covarianza pendientes aleatorias
#sigma_e: varianza error

#L_u[i,j]: las necesito para crear R[i,j]***



# ==============================================================================
# SECTION 5.b: Posterior Predictive Model Check (PPMC) MODELO 1 
# ==============================================================================

# Extraer y_rep correctamente desde CmdStanR
y_rep_2 <- as_draws_matrix(bmultinivel_2f$draws("y_rep"))

# Seleccionar solo 100 iteraciones aleatorias (iteraciones)
set.seed(123)  # Para reproducibilidad
y_rep_subset_2 <- y_rep_2[sample(1:nrow(y_rep_2), 100), ]

# Verificar dimensiones
dim(y_rep_subset_2)  # Debería ser (100, 300)

# Número de colegios
J <- length(unique(data_stan$schid))

# Lista para almacenar los gráficos
posterior_plots_list_2 <- vector(mode = "list", length = J)

# Generar gráficos PPMC para cada colegio
for(j in 1:J){
  posterior_plots_list_2[[j]] <- ppc_dens_overlay(
    y = data_stan$math[data_stan$schid == j],        # Datos reales del colegio j
    yrep = y_rep_subset_2[, data_stan$schid == j]  # Simulaciones para colegio j
  ) + 
    labs(title = paste("Colegio", j))
}

# Mostrar los gráficos juntos
cowplot::plot_grid(plotlist = posterior_plots_list_2)


# ==============================================================================
# SECTION 5.c: Comparacion de modelos (capacidad predictiva)
# ==============================================================================

loo_1f  <- loo(x = bmultinivel_0f$draws("log_lik"))
loo_2f  <- loo(x = bmultinivel_1f$draws("log_lik"))
loo_3f <- loo(x=bmultinivel_2f$draws("log_lik"))
loo_compare(loo_1f, loo_2f, loo_3f)